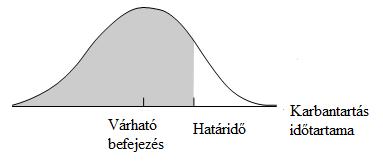
1. sz. ábra
A karbantartás várható befejezésének és határidejének ábrázolása normál eloszlásban
Stifter Tamás
minőségügyi mérnök csoportvezető
Lufthansa Technik Budapest Kft.
tamas.stifter@lhtb.hu
Az operációkutatás, mint tudományág felhasználása légijármű karbantartásban – 2. rész
(Basics of the application of Operations Researh in aviation maintenance – Part 2)
REZÜMÉ
A cikksorozat első részében a legegyszerűbb operációkutatási módszereket vizsgáltam meg a légijármű karbantartás, mint tervütemháló optimálására. A kritikus út módszerét, valamint a PERT módszert. Most e két módszer kombinációjának nevezhető CPM/Cost módszert vizsgáljuk meg, amely lehetőséget ad mind időben, mind költségek tekintetében optimálni.
RESUME
In the first article of the series the most simple methodes of the operations research were examined to optimize the aircraft maintenance process as a network. The CPM and the PERT methodes were reviewed. Now We examine the CPM/Cost method which is a combination of the above mentioned methodes and gives possibility optimize the timing and cost of activities.
NETWORK (TERVÜTEMHÁLÓ) OPTIMALIZÁLÁSÁNAK LEHETŐSÉGEI (FOLYTATÁS)
A cikk első részében két módszert vizsgáltam meg: a kritikus út módszerét1 és a PERT2 módszert. Ezeket a módszereket az 50-es 60-as években használták bonyolult munkafolyamatok például nagyobb építkezések és repülőgép összeszerelés folyamatainak optimálására. A kritikus út módszerének továbbfejlesztése az angol terminológiában PERT/CPM[1], illetve CPM/Cost-nak (kritikus út/költség) [3] nevezett módszer.
A hálóterv kritikus útjának meghatározása után további kérdések merülhetnek fel. Például az, hogy a PERT módszernél figyelembe vett optimista, legvalószínűbb és pesszimista tevékenységi idők figyelembevételével, vajon milyen valószínűséggel lehet befejezni például egy karbantartást az elvárt vagy szerződött határidővel. Ezt a következő módon ábrázolhatjuk:

1. sz. ábra
A karbantartás várható befejezésének és határidejének ábrázolása normál eloszlásban
Standard normál eloszlást figyelembe véve, a karbantartás határidőre befejezésének valószínűsége a következőképpen írható fel:
![]()
ahol T – a karbantartás időtartama, d – a karbantartás befejezésének határideje.
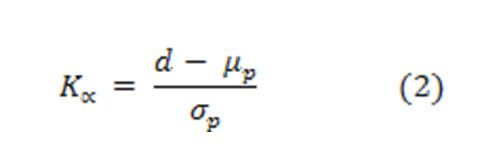
ahol - a karbantartási tevékenységek várható idejének kummulatív értéke, vagyis a karbantartás teljes várható ideje. Értékes információ nyerhető ezáltal, hiszen például a szórás növekedése esetén értéke csökken, és ezáltal a határidőre történő befejezés valószínűsége is csökken. Ezt az üzleti döntéseknél figyelembe is lehet venni, de önmagában nem ad megfelelő támogatást döntésekhez.
Jelenleg az irányadó trend az átfutási idő csökkentése mindenáron. Erre nagy igény is van napjainkban, hiszen a repülőgép karbantartással foglalkozó cégeknek folyamatosan a TAT3 rövidítését kell biztosítani az ügyfelek megelégedésére. Időmegtakarításra mód csak akkor van, ha egy-egy tevékenység várható idejét rövidítjük le. Itt azonban látnunk kell, hogy a tevékenységek idejének rövidítése minden esetben költség növekedéssel jár.
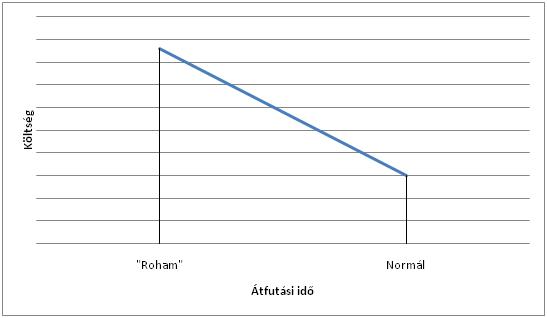
2. sz. ábra
Átfutási idő költség függvény [1]
A 2.sz. ábrán látható függvény minden egyes hálótervben szereplő tevékenységhez felírható konkrét idő és költségadatok meghatározása mellett. Itt kizárólag a közvetlen költségeket vesszük figyelembe, valamint fontos az is, hogy a közvetlen költség alakulását a tevékenység elvégzéséhez szükséges idő vonatkozásában lineáris függvénynek tekintjük. A függvény értékeinek figyelembevételével minden tevékenység egy-egy átfutási idejéhez a normál és a „roham”4 munkavégzési módok közt meghatározható annak költsége. Másképpen fogalmazva kiszámítható egy-egy tevékenység tekintetében az átfutási idő csökkentésének költsége.
Itt figyelembe kell vennünk a témában írt előző cikk megállapítását, miszerint: „A kritikus útvonal vonatkozásában az igaz, hogy annak rövidítése az egész komplex rendszer befejezési határidejére hatással lesz, de csak addig, amíg nem jelenik meg egy újabb kritikus út a rendszerben.” [2] Nyilván abban az esetben, ha egy tevékenység idejének csökkentése során a hálótervben másik kritikus út jelenik meg, akkor az ahhoz az úthoz tartozó tevékenységeket kell megvizsgálni átfutási idő csökkentése tekintetében.
Ekkor a hálóterv egészének optimálását tekintve az a feladat, hogy megtaláljuk, hogy mely folyamat átfutási idejét kell csökkentenünk. Az esetünkben azt vizsgáljuk meg, hogy a lehető legkisebb költséggel érjünk el egy adott értékű átfutási idő csökkentést.
A feladat megoldásának algoritmusa[3]:
Eltérően az első részben[2] megvizsgált CPM feladattól a tevékenységi időt τ(x,y) két korlát között vehetjük fel:
![]()
Ahol a(x,y) a „roham” munkavégzés tevékenységi ideje, míg b(x,y) a normál munkavégzés tevékenységi ideje.
Ahogy az az 1. sz. ábrán is látható a normál tevékenységi időhöz kapcsolódik a minimális, a „roham” munkavégzés tevékenységi idejéhez kapcsolódik a maximális költség. Így a τ(x,y) tevékenységi időhöz tartozó költség lesz. Így a feladat egy olyan terv ütemezés megadása, ahol:
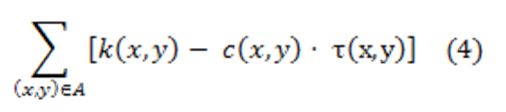
költség minimális. Mivel a
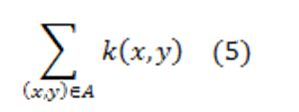
költség összetevő egy konstans érték, hiszen az a „roham” munkavégzéshez tartozó költségek összessége. Ezért a minimális költség elérése a
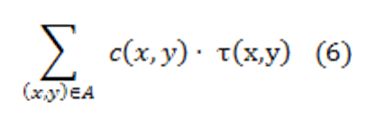
változó költségösszetevő maximalizálásával ekvivalens. Így a költségtervezés feladata a következőképpen írható fel matematikailag:
Adott [N,A] tervütemháló, amelynek (x,y) élein adottak a(x,y) ≤ b(x,y), valamint c(x,y) nem negatív egész értékek.
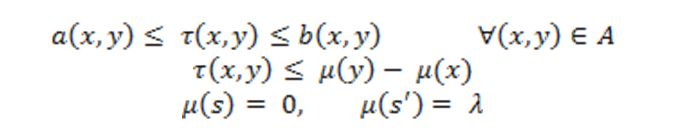
Ezen feltételek mellett maximalizálni kell a következő haszonfüggvényt:
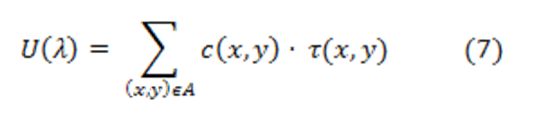
Ahol λ az egész munkafolyamat átfutási idejét (TAT) jelenti, amelyet ebben az esetben előre meg kell adni, hiszen ezt is tekintjük feladatunknak. Azt szeretnénk meghatározni, hogy mely módon lehet a legkisebb befektetéssel az előre meghatározott időben befejezni a karbantartási műveletet.
Határozzuk meg, hogy mindez hogyan hozható kapcsolatba egy folyamproblémával. Legyen µ(x) és τ(x,y) függvény megfelelő a már definiált folyamatnak, és az [N,k] hálózaton egy tetszőleges s-ből s’-be irányuló F folyam. Akkor a következő egyenlőtlenség írható fel:
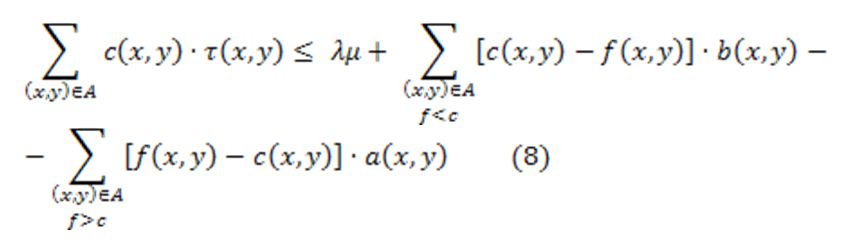
Ebben az egyenlőtlenségben akkor lehetséges egyenlőség, ha a bal oldal maximum és a jobb oldal minimum értéket ér el. Az egyenlőség fennállásához a τ(x,y) és a µ(x,y) értékeknek optimalizálniuk kell f haszonfüggvényt, amelyre igaz és elégséges feltétel, hogy:
Ebből láthatjuk figyelembe véve az (7) számú képletet, hogy az U(λ) haszonfüggvény maximalizálása miatt elegendő a
![]()
értékre szorítkozni.
Tehát a megvizsgált CPM/Cost módszer komplexebb a korábban megvizsgált CPM és PERT módszereknél[2]. Fontosságot tulajdonít mind a befejezési időpontnak, mind pedig a költségek alakulásának. Azonban egy légijármű időszakos karbantartási folyamat optimálása ennél több változó figyelembevételét követel(het)i meg.
FELHASZNÁLT IRODALOM - irodalmi hivatkozások:
[1] – McGraw-Hill: Introduction to Operations Research, 7th Edition. [2000., ISBN0072321695]
[2] – Stifter Tamás: Alapok az Operációkutatás, mint tudományág felhasználásához légijármű karbantartásban, Repüléstudományi Közlemények, Szolnok 2009/4
[3] – Glevitzky Béla: Operációkutatás II. mobiDIÁK könyvtár, 2003
1 Kritikus út módszere, az angol nyelvű irodalomban CPM – Critical Path Method vagy másutt CPM/time-ként utalnak rá, mert kizárólag az időtartammal foglalkozik
2 PERT módszer – Program Evaluation and Review Technic. Ennél a módszernél a tevékenységi időket egy valószínűségi változónak tekintjük, és ennek segítségével tervezzük a végrehajtási határidőt.
3 TAT - Turn Around Time, vagyis a légijármű karbantartásának átfutási ideje
4 „Roham” munkavégzés alatt az adott tevékenység végrehajtásának lehető legrövidebb idejű végrehajtását értjük