Jelen cikk a Repüléstudományi Konferencia 2009 Szolnok 50 év hangsebesség felett a Magyar légtérben megjelent „Nyitott vízszintes alapú inerciális navigációs rendszerek” [1] egyenleteit és ábráit felhasználva a zárt vízszintes alapú inerciális navigációs rendszereket mutatja be.
A nyitott inerciális navigációs rendszerekben, amelyek a vízszintes koordináta-rendszerben működnek (az alap, amelyen az axelerométerek voltak), a vízszintes síkban stabilizálódott a rajta elhelyezett axelerométerek mutatásainak használata nélkül, valamilyen fedélzeti függőlegesek segítségével. Ehhez, mint azt láttuk a 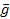 vektor figyelembe vétele vezetett .
A zárt inerciális navigációs rendszerben, amelyek a vízszintes koordináta rendszerben működnek, amikor a 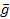 vektorról semmiféle információ a különféle fedélzeti műszerekről nem feltételeződik, a  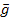vektor kompenzálása a vízszintes síkban az alap stabilizálásával, az axelerométerek mutatásának segítségével történik, amelyek magán az alapon vannak elhelyezve.
Lehetséges-e ilyen stabilizáció? Megmutatjuk, hogy lehetséges. Először megmagyarázzuk az ilyen stabilizáció lényegét a zárt inerciális navigációs rendszerek példáján, amely vízszintesen azimutálisan szabad koordináta-rendszerben működik.
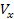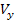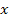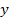Legyen az azimutálisan szabad alap a kezdeti időpillanatban vízszintes. Továbbá az objektum mozogjon  és  sebességgel az  és  tengelyek mentén. (1. ábra)

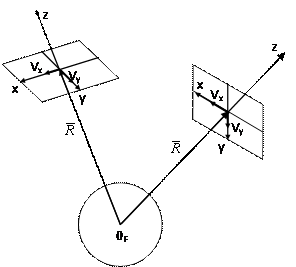
1. ábra.
Ha valamilyen úton módon az alapot elfordítjuk az x tengely körül

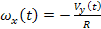      (1)

szögsebességgel és az y tengely körül

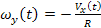       (2)

szögsebességgel, akkor az alap továbbra is vízszintes marad (1. ábra)
A szükséges szögsebesség értékek kiszámítása az alap elfordulásával (1), (2) egyenletekből a 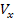 és 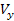 jelekkel egyetértve, amelyeket az axelerométerek  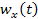és 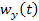 mutatásának integrálásával a  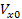és 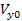 kezdeti feltételek alapján lehet meghatározni.
A gyakorlatban hogyan lehetséges az alap elfordulását a kiszámított szögsebességekből 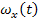 és 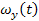 megvalósítani?
Nagyon egyszerű, ilyen elfordulásokat kétszabadságfokú pörgettyű segítségével lehet megvalósítani, amelyek az alapon úgy vannak elhelyezve, mint ahogyan azt a 2. ábrán láthatjuk.

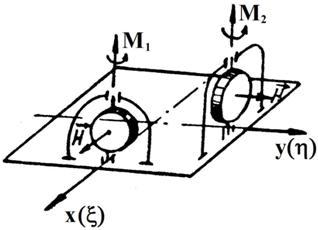
2. ábra.

Ha a pörgettyű körül 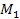 és 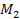 nyomatékkal hatunk, amely a repülőgépen háromszabadságfokú kardánfelfüggesztésben van elhelyezve, részt vesz a pörgettyű precessziós mozgásában

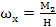       (3)
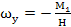      (4)

szögsebességgel.
Ha 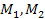-t az ismert  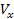és 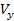 alapján hozzuk létre, akkor

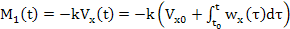      (5)
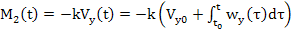       (6)

és a k arányossági tényezőt a 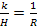 feltételből határozzuk meg:

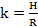      (7)
akkor a (3) - (7) egyenletekből kapjuk, hogy az alap szögelfordulásának forgása:

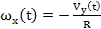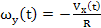;        (8)

összehasonlítva a (1) és (2) egyenleteket a (8) egyenlettel azt kapjuk, hogy az ilyen alap mindig vízszintes marad. A (7) kifejezést Schuler-feltételnek nevezzük.
Tehát a következő eredményt kaptuk: Legyen egy pörgettyűs alap, amely a 2. ábrán látható. Ha elhelyezünk rajta két axelerométert és a giroszkópok tengelyeire nyomatékot rakunk, amely az integrállal arányos és az axelerométerek mutatásától a sebesség kezdeti feltételeinek figyelembe vételével, akkor abban az esetben, ha az arányossági tényező eleget tesz a Schuler feltételnek, az alap, amely a kezdeti időpillanatban vízszintes helyzetben van, vízszintes is marad a repülőgép maradék mozgása során.
Ebben az esetben a vízszintesen azimutálisan szabad alapon elhelyezett axelerométerek jelzései a 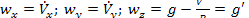egyenlet alapján:

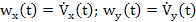      (9)

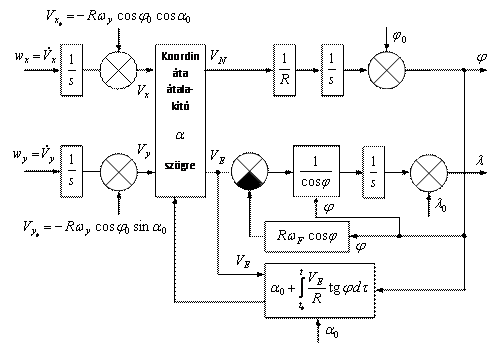
3. ábra
Nyitott vízszintes alapú azimutálisan szabad inerciális navigációs rendszerhatásvázlata [3]
[Szerk.: Dr. Békési Bertold – MS Word]

Ha ezeket a jeleket bevezetjük a 3. ábrán látható számító egységbe, akkor meghatározható a repülőgép sebessége és a földrajzi koordinátái. Az ilyen inerciális rendszer egyértelműen zárt lesz.
Mi is tehát a különbség a nyitott vízszintesen azimutálisan szabad inerciális navigációs rendszertől? Az eltérés a következő:

• az alap vízszintesben tartásához külső jelzést használ fel (nyitott inerciális navigációs rendszer);
• az axelerométerek jelzéseit használja fel a vízszintesben tartásra (zárt inerciális navigációs rendszer).

Tárgyaljuk meg a kapott eredményt:
Először a giroinerciális alap vízszintes marad az objektum bármilyen pályájú mozgása során. Ilyen esetben azt mondják, hogy a giroinerciális alap ballisztikusan stabilis. Ez a sajátossága a giroinerciális alapnak. Elemezhetjük mint előnyét, összehasonlítva a műhorizontokkal és a pörgettyűs mesterséges műfüggőlegesekkel, sugárirányú helyesbítéssel, amelyek az objektum manőverezése során igen nagy hibával rendelkeznek.
Másodsorban, a zárt giroinerciális navigációs koordináta rendszer folyamatosan méri és számítja az objektum olyan fontos mozgási paramétereit, mint a gyorsulás, a sebesség és a koordináták. Mindezek a mérések teljesen autonóm módon mennek végbe, vagyis nem igényelnek semmilyen földi berendezést, amelyek ezt a munkát biztosítanák. Innen származik a zárt inerciális navigációs rendszer teljes zavarvédelme.
Ha a zárt inerciális navigációs rendszer működési elvének vizsgálatakor a figyelmünket mi csak a giroinerciális rendszerek olyan mozgására fordítottuk, amikor a kezdeti időpillanatban az alap vízszintes volt és minden kezdeti feltétel abszolút helyesen volt bevezetve, tehát csak a rendszer zavarvédett mozgása volt megvizsgálva.
Felmerül a kérdés, hogyan fog mozogni a rendszer, ha a kezdeti időpillanatban az alap nem volt vízszintes és a kezdeti feltételek hibával voltak bevezetve? Tehát felmerül a stabilitás működésének kérdése is a zárt giroinerciális navigációs rendszerekben.
Ezenkívül nagyon fontos megvizsgálni a giroinerciális rendszerek hibáit, amelyek az elemek szerkezeti hibájából lépnek fel:

• a pörgettyűk eltávozása az alaptól;
• az integrátorok hibái.

És végezetül megemlíteném, hogy mi csak a zárt vízszintesen azimutálisan szabad giroinerciális navigációs rendszert vizsgáltuk.
Fontos megvizsgálni a zárt giroinerciális navigációs rendszereket más típusú alapokkal is. Ezenkívül lehetséges olyan zárt inerciális navigációs rendszer, amikor az axelerométerekkel, szögsebességekkel (1), (2) egyenletek az alap elfordulásának szükségessége nem a giroszkópok segítségével történik, hanem a teleszkópos berendezések segítségével, amelyek a csillagokra vannak irányítva. Az ilyen zárt inerciális navigációs rendszereket asztroinerciális rendszereknek nevezzük.
Mindezen kérdésekre majd később válaszolunk. Ezen cikk befejezésekor bemutatom a zárt inerciális rendszert azimutálisan szabad alappal (4. ábra).
Az alap kardánfelfüggesztésben van elhelyezve. Ennek következtében a kardánfelfüggesztés külső keretének tengelye egybeesik a repülőgép hosszirányú tengelyével, a belső keret tengelye vízszintes és az alap tengelye függőleges. A kardánfelfüggesztés tengelyének csak ilyen elhelyezése teszi lehetővé a repülőgép bedöntési 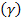, bólintási  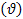és irányszög  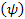kardánhibák nélküli mérését.
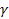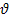A bedöntési, bólintási és irányszögek a 4. ábrán 13, 14, és 15 jelölik. Megjegyezzük, hogy az ilyen alapot nem lehet elhelyezni a repülőgépen korlátlan manőverező képességgel. Ahhoz, hogy elhelyezhessük az alapot a repülőgépen, a külső keretet egy követő keretbe kell elhelyezni, amelynek tengelye egybe kell, hogy essen a repülőgép hossztengelyével. A  (13),  (14) és  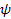(15) adók a kardánfelfüggesztés tengelyein vannak elhelyezve.
Az alapon elhelyezett (1 és 5) pörgettyűk az alapot a vízszintes síkban tartják meg és a (16) iránypörgettyű az alap azimutális helyzetét vezérli. Ha az iránypörgettyű nem kerül helyesbítésre, akkor azimutálisan szabad lesz és az alap szintén azimutálisan szabad lesz. A (3, 7) axelerométerek jelzései a (4, 8) integráló berendezések integrálása után az (1, 5) pörgettyűk (2, 6) nyomatékmotorjaira kerülnek. A csatorna erősítési tényezőjét az axelerométertől a pörgettyű nyomatékmotorjáig a Schuler feltételből állapítjuk meg.

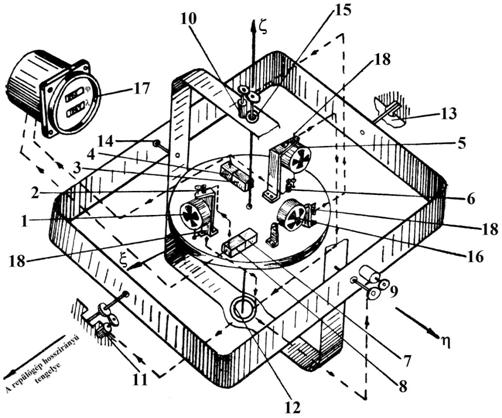
4. ábra
Zárt inerciális rendszer azimutálisan szabad alappal [3]

Az alap valamennyi tengelye mentén (3 tengely) tehermentesítve van. A tehermentesítő rendszer részei:

• 3 db szöghelyzetadó (18);
• sinus-cosinus koordináta átalakító (12);
• végrehajtó tehermentesítő motorok (9, 10, 11);
• az integrátorok jelzései, amelyek a sebesség értékével egyenlőek 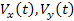 a (17) megoldó egységbe kerülnek, amely a 3.ábrán látható;
• a megoldó egység a repülőgép földrajzi koordinátáinak 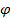 és 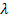 kiszámítását végzi.

Még egyszer összefoglalva:

• a giroinerciális alap kiváló girofüggőleges, amely nem rendelkezik ballisztikus deviációval (bármilyen mozgáspályán vízszintes marad);
• teljesen autonóm, vagyis nem igényel földi eszközöket, amelyek biztosítanák a munkát. Ebből következik a zárt inerciális navigációs rendszer teljes zavarvédettsége.

A vizsgált rendszer előnyei:

• kiválóan alkalmas a 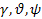 kardánhibák nélküli szögmeghatározásra;
• a giroinerciális rendszer lehetővé teszi majdnem minden fedélzeti-navigációs paraméter mérését: bedöntés, bólintás, irányszög, útsebesség és a koordinátákat.

A vizsgált rendszer hátránya:

• az objektum koordinátáinak mérési hibái az inerciális rendszer működési idejének függvényében növekednek.

¹ Repüléstudományi Konferencia 2009 Szolnok 50 év hangsebesség felett a Magyar légtérben megjelent „Nyitott vízszintes alapú inerciális navigációs rendszerek” cikk alapján.
² Repüléstudományi Konferencia 2009 Szolnok 50 év hangsebesség felett a Magyar légtérben megjelent „Nyitott vízszintes alapú inerciális navigációs rendszerek” cikk 2. ábrája alapján.
³ A repüléstudományi Közlemények 2008/3 számában megjelent Inerciális navigációs rendszerek II. cikkben részletesen elemezve.

Felhasznált irodalom
[1] Dr. Békési Bertold: Inerciális navigációs rendszerek II. Repüléstudományi Közlemények online folyóirat, Szolnok, 2008/3 szám. HU ISSN 1789-770X
[2] Dr. Békési B. — Dr. Szegedi P. Nyitott vízszintes alapú inerciális navigációs rendszerek. Repüléstudományi Közlemények különszám, Szolnok, 2009. április 24.
[3] В. А. Вериго, Ф. С. Гергель: Пилотажно-навигационные приборы и измерительные системы. Ленинградская Краснознаменная военно-воздушная инженерная академия имени А. Ф. Можайского, Ленинград, 1959.

Vissza a tartalomhoz >>>