Dr. Békési Bertold
ZMNE BJKMK Repülő és Légvédelmi Intézet Fedélzeti Rendszerek Tanszék
bekesi.bertold@uni-nke.hu

A Repüléstudományi Közlemények 2008/2 számában megjelent Inerciális navigációs rendszerek I. folytatásaként a cikkben a gyorsulásmérők alapegyenleteit vizsgálom meg a forgó és nem forgó koordináta rendszerben, valamint a Schuler-ingát.

1. A gyorsulásmérők egyenletei. A Schuler-inga.
1.1 Az ideális gyorsulásmérők egyenletei a nem forgó koordináta rendszerben

Az vektor abszolút gyorsulása egyenlő az  rádiusz vektor második deriváltjával az idő szerint¹ az inerciális rendszerhez képest

(1 sz. egyenlet)

Ha valamely előre kiválasztott inerciális koordináta rendszer egységvektorai  az  nem forgó koordináta rendszer egységvektoraira kollineárisak, akkor

Az előzőből következik

(2 sz. egyenlet)

ahol:

 - az  második deriváltja az  koordináta rendszerhez képest
Világos, hogy az (2) egyenletnek van értelme az  és  koordináta rendszerek tengelyeinek bármilyen elhelyezkedése esetén, mivel az (2) értelme abból következik, hogy az  koordináta rendszer  szögsebessége egyenlő nullával.
Így az axelerométerek mozgásegyenlete megegyezik alakilag az inerciális koordináta rendszerben felírt egyenletrendszerrel a nem forgó koordináta rendszerben.

 (1 sz. egyenlet)

vagy koordinátás alakban

 

(4 sz. egyenlet)

Tehát, ha az axelerométerek valamilyen berendezés segítségével az  nem forgó koordináta rendszer tengelyei mentén lennének elhelyezve, akkor az ő jelzéseik  a (4) egyenlettel lenne egyenlő (vagy másképpen a (4) egyenletrendszer megadja az axelerométerek jelzéseit abban az esetben, ha azok tengelyeit a nem forgó koordináta rendszer tengelyei szerint állítjuk be).
Az axelerométerek stabilitása az  nem forgó koordináta rendszer tengelyei mentén elérhető, például úgy, hogy elhelyezzük őket egy alapra, a térben teleszkópok segítségével stabilizálva, amelyek a csillagokra vannak orientálva vagy szabad giroszkópok (pörgettyűk) segítségével. Világos, hogy az objektum  rádiusz-vektorának, vagyis az ő három vetületének, , ,  teljes egészében megoldja a navigációs feladatot az objektum koordinátáinak meghatározását a Földhöz képest. (Később majd bemutatjuk, hogyan lehet a rádiusz-vektortól  áttérni az objektum földrajzi koordinátáihoz: a szélességéhez és a hosszúságához, valamint a többi koordinátához).
Az  illetve annak tengely vetületeit meghatározva megkapjuk a repülőgép tartózkodási helyének koordinátáit. Az  meghatározható az axelerométerek  jelzése alapján (amely az axelerométerektől jön, nem forgó alapon van elhelyezve) két módszer szerint lehet végrehajtani.
Az első megoldásnál abból indulnak ki, hogy valamilyen műszerek segítségével, amelyek a mozgó objektum fedélzetén vannak elhelyezve, az axelerométereken kívül a fedélzeten ellenőrző műszerek segítségével meghatározható  vektor. Így például a  vektor a repülőgép fedélzetén megállapítható, az iránya valamilyen műszer szerinti függőleges segítségével, értéke szerint pedig ezt a vektort a földközeli repüléseknél állandónak vehetjük és egyenlő .
A Földtől nagyobb távolságban a  vektor értékét tekintve a magasságmérő segítségével számíthatjuk ki az ismert formula alapján , ahol  - a Föld tömegvonzásának állandója.
Ebben az esetben a repülőgép rádiusz-vektora  és a repülőgép fedélzetén a gravitációs mező intenzivitása esetében  és az ismert kezdeti feltételekből  és  megkaphatjuk, ha az (4) egyenletből kiindulunk, tehát:

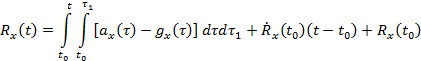
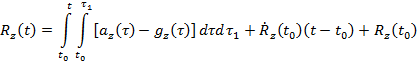(5 sz. egyenlet)

Az inerciális navigációs rendszerek amelyben a mozgó objektum koordinátái (az  rádiusz vektora), az axelerométerek mutatása alapján lehet meghatározni, amely stabilizált alapon van elhelyezve más ismert műszerektől, kivéve az axelerométereket, a gravitációs mező intenzivitásának  vektorával, nyitott navigációs rendszernek nevezzük.
Áttérünk a második módszer tárgyalására.
Megállapítható-e az  rádiusz vektor a mozgó objektum axelerométereinek mutatása alapján, amelyek a nem mozgó alapon vannak elhelyezve, ha az objektum tartózkodási pontjában a gravitációs mező  intenzitásáról nincs semmilyen információnk.
Valóban ha feltételezzük, hogy a repülőgép a centrális (központi) gravitációs mezőben mozog, akkor a  vektort az -n keresztül kaphatjuk meg.

 (6 sz. egyenlet)

Ebben az esetben az axelerométerek egyenlete, amely nem forgó alapon van elhelyezve a következő képpen írható fel:

 (7 sz. egyenlet)

Az (7) egyenletből amely vektoriális alakban van felírva kapjuk, hogy a keresett objektum  rádiusz vektora a következő integrális alak formájában írható fel:

 (8 sz. egyenlet)

Az (8) egyenlet koordinátás alakban a következő:

 
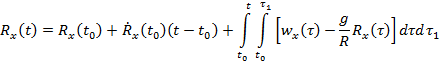
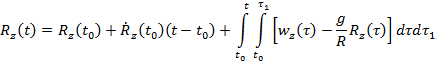(9 sz. egyenlet)

Az  meghatározására a (9) egyenletből a következő hatásvázlat rajzolható fel (1. ábra), ahol

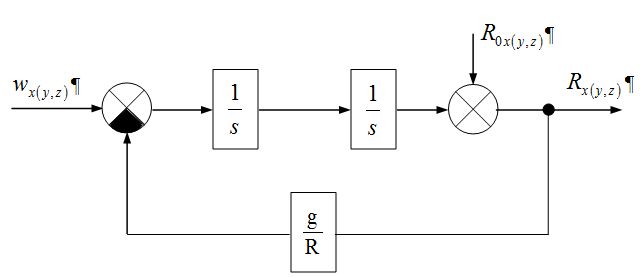
1. ábra. Hatásvázlat az  meghatározására

Ez a hatásvázlat három csatornával rendelkezik, amely az  rádiusz vektor minden egyes vetületének a kiszámítására megfelel. Ha csak a földközeli navigációt vizsgáljuk, amikor az objektum repülési magassága a Föld  rádiuszához (sugarához) képest annyira kicsi, hogy a  érték változása nem haladja meg az 1-3%-ot, akkor az 1. ábra visszacsatolási állandója (tényezője), amely egyenlő , ahol  - a gravitációs mező intenzivitása a Föld közelében.

Figyelembe véve, hogy a

akkor kapjuk, hogy ha a  vagy  akkor a  érték nem változik több mint 1-3%-kal.
Ebben az esetben az objektum  rádiusz vektorának a kiszámítása, csak az axelerométerek  mutatása (jelzése) alapján történik, amelyek a nem forgó alapon vannak elhelyezve, más műszerek mutatásának bevonása nélkül a számító egység segítségével, amelynek a hatásvázlata az 1. ábrán látható állandó visszacsatolási tényezője esetén, amely egyenlő .
Ez a számító egység három csatornával rendelkezik, amelyek közül mindegyik egy lengő tag amely a stabilitás határán van.
A lengések körfrekvenciája:

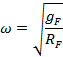
Ezen lengések periódus ideje:

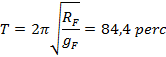
amelyet Schuler-periódusnak szokás nevezni.
Az inerciális navigációs rendszerek, amelyekben a mozgó objektum koordinátái (az  rádiusz vektora) csak az axelerométerek mutatása alapján lehet meghatározni, amely stabilizált alapon van elhelyezve, ekkor a gravitációs mező  vektorának intenzivitása kompenzálódik az objektum koordinátáinak a kiszámított axelerométerek mutatásának segítségével.

A

zárt inerciális navigációs rendszernek nevezzük.
Tehát a következő eredményt kaptuk:
A zárt inerciális navigációs rendszerben az objektum pillanatnyi koordinátáinak meghatározása az axelerométerek jelei alapján történik, amelyek stabilizált alapon vannak elhelyezve az inerciális térhez képest, a lengő tagok bemenetére, amelyek saját lengéseinek periódusa .

Ekkor ezen tagok kimenetén a jelek a mozgó objektum  rádiusz vektorának vetületeivel lesznek egyenlőek . Ez az utóbbi állítás a Schuler-tétel elnevezést viseli.
Megjegyzés:
Az inerciális navigációs rendszer mint a nyitott, úgy a zárt típusa három alapvető elemet tartalmaz:

• axelerométer egységet;
• koordináta rendszert realizáló berendezést a repülőgép fedélzetén (ebben az esetben nem forgó koordinátarendszert);
• számító egységet.

A zárt inerciális koordináta rendszer számító egysége egy dinamikai rendszert mutat be (lengő tag), amely a stabilitás határán helyezkedik el. Ez nem a számító egység technikai megvalósításával van kapcsolatban, hanem a zárt inerciális rendszer munkájának létezésével. Ez az axelerométer alapvető egyenletéből következik. Később majd lesz róla szó, hogy ez a helyzet a reális inerciális navigációs rendszerek munkájának minőségére nincs nagy hatással.
Végül megemlítjük, hogy mint a nyitott, úgy a zárt inerciális navigációs rendszerek esetében az axelerométerek, nem feltétlenül szükséges, hogy stabilizált alapon legyenek elhelyezve. Bármilyen alapon el lehet őket helyezni, amelyek az objektumon vannak, bármilyen térbeli mozgást feltételezve, tehát akár az objektumon is elhelyezhetők.
Ekkor a mutatások (jelzések) vektorai², bármilyen elhelyezési módszer alapján egyenlőek lesznek és .
De ebben az esetben szükség van egy berendezésre, amely az axelerométerek mutatása  alapján, ha az objektum fedélzetén a nem mozgó koordináta rendszer megvalósításával kiszámolnánk a  vektor  vetületeit ezen koordinátarendszer  tengelyeire.

A további vizsgálódásaink során, nem fogjuk mindig megbeszélni ezt a helyzetet és figyelembe kell venni, hogy a kifejezés: "az axelerométerek, amelyek az alapon vannak elhelyezve és az  koordináta rendszerhez képest stabilizálva vannak" nem szó szerint kell értelmezni, hanem azon értelmezés alapján, hogy az axelerométerek az alaptól külön is elhelyezhetők. Elsősorban a számító egység segítségével határozzuk meg a  vektor  vetületeit.
1.2 A Schuler-inga
A zárt inerciális navigációs rendszerek hibája az alap pontatlan stabilizálásából ered. Ez arra vezethető vissza, hogy a függőleges irányt megadó inga nem a valódi, hanem a látszólagos függőleges irányába áll be. Szükségessé vált olyan inga alkalmazása, amelyet az alapra ható gyorsulások nem zavarnak Ezt először Max Schuler 1923-ban fogalmazta meg.
Az ilyen inga egyensúlyi helyzetbe beállítva, attól akkor sem tér el, ha a felfüggesztési pontra gyorsulások hatnak, így ez az inga mindig a valódi függőleges irányt adja meg. A 2. ábrán az  - az inga elfordulása a tengely felfüggesztése körül. Az egyszerűsítések feltételezése végett:

• a felfüggesztési pont  gyorsulással mozog a nagy kör mentén;
• a földet gömb alakúnak fogjuk fel, és a vonzásmezejét központinak (centrikusnak) vagyis a  a Föld középpontja felé mutat;
• feltételezzük, hogy a Föld nem forog;
• az inga lengési síkja egybeesik a mozgás síkjával.

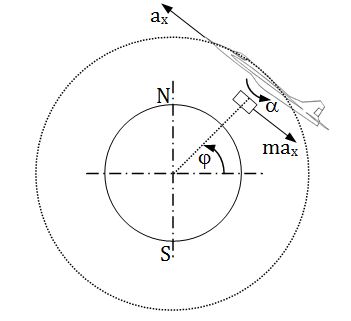
2. ábra

Az inga mozgását leíró differenciál egyenlet:

(10 sz. egyenlet)

ahol:
             - az inga tömege
               - a felfüggesztés tengelye és az inga tömegközéppontjának távolsága
- az inga elfordulásának szöggyorsulása
               - az inga inerciális nyomatéka a felfüggesztési tengelyhez képest

Az inga elfordulásának szöggyorsulása:

   (11 sz. egyenlet)

A felfüggesztési pont mozgása során a pontot a föld középpontjával összekötő függőleges irány szöggyorsulása

(12 sz. egyenlet)

hányadossal határozható meg, ha a repülési magasságot a Föld sugarához képest elhanyagoljuk .
Ahhoz, hogy a gyorsuló mozgások esetén a felfüggesztés tengelye mindig megegyezzen a függőleges iránnyal, az inga elfordulásának szöggyorsulása meg kell hogy egyezzen a függőleges elfordulásának szöggyorsulásával
Ebben az esetben

(13 sz. egyenlet) 

A (13) egyenlet független a felfüggesztési pontra ható gyorsulástól. A fizikai inga lengési ideje:

(14 sz. egyenlet)

Mivel a (13) egyenletből  ezért

(15 sz. egyenlet)

Ha  akkor az inga lengési periódusideje 84,4 perc.

Az inga helyzetét a felfüggesztésre ható gyorsulások az inga helyzetét nem fogják befolyásolni. Ez a Schuler-inga. Gyakorlatilag ilyent létrehozni nem lehet (ezért módszereket dolgoztak ki például: pörgettyűs berendezések segítségével lehet őket modellezni).

2. Az axelerométerek alapegyenletei a forgó koordináta rendszerben
Valamilyen  koordináta rendszer forogjon  szögsebességgel az inerciális térben. Mint ismeretes, bármely vektor  abszolút deriváltja, ugyanezen vektor végének abszolút sebességével reprezentálható. Ez a sebesség áll a relatív sebességből  és az átvitt sebességből .

Következésképpen az  vektor abszolút deriváltja, amelyet a továbbiakban -vel jelölünk, felírhatjuk a következő alakban:

(16 sz. egyenlet)

ahol:   - az  deriváltja az  koordináta rendszerhez képest
Ebben az esetben a  abszolút deriváltjára az  rádiusz vektorból kapjuk:

(17 sz. egyenlet)

Még egyszer felhasználva a (15) egyenletet a  vektorhoz, kapjuk:

           
(18 sz. egyenlet)

A (18) egyenletet elementáris átalakítások után a következő alakban írható fel

(19 sz. egyenlet)

ahol:
 - pillanatnyi forgó gyorsulásvektor az  koordináta rendszerhez képest.

A (19) egyenletben a  differenciálási szimbólum a viszonylagos  koordináta rendszer deriváltját jelenti.
A (19) egyenletet Coriolis elvnek hívják. Az egyenlet jobb oldalán minden vektor deriváltját az  viszonylagos koordináta rendszerhez képest vizsgáljuk.
A (19) egyenlet alapján megkapjuk az axelerométer alapegyenletét a viszonylagos koordináta rendszerben, amely az inerciális térben  szögsebességgel forog.

  (20 sz. egyenlet)

A (20) egyenletben úgy, mint a (19) egyenletben, minden deriváltat az  viszonylagos koordináta rendszerhez képest vizsgáljuk, ezért az axelerométerek egyenletét (20) az axelerométerek egyenletének nevezik a viszonylagos (forgó) koordináta rendszerben.
Megjegyezzük, hogy az elméleti mechanikában a  tagot viszonylagos gyorsulásvektornak, a  tagot a Coriolis gyorsulásvektornak és az tagot átvitt gyorsulásvektornak hívják.
A továbbiakban áttérünk az axelerométerek egyenleteire a konkrét koordináta rendszerekben.

3. A gyorsulásmérők egyenletei a vízszintes földrajzi koordináta rendszerben
Tételezzük fel az egyszerűség kedvéért, hogy a repülőgép mozgása közel állandó magasságon történik, vagyis , amelyen egy vízszintes földrajzi alap és axelerométer van elhelyezve. Ebben az esetben figyelembe véve, hogy az  mindig megegyezik az  vízszintes földrajzi koordináta rendszer z tengelyével. Ekkor az  deriváltja a kiválasztott koordináta rendszerben

A (20) egyenletből akkor következik:

              (21 sz. egyenlet)

A 4. ábrából³ megkaphatjuk, hogy az az  forgó vízszintes földrajzi koordináta rendszer pillanatnyi sebességének vetülete egyenlő:

 (22 sz. egyenlet)

ahol:
      - a repülőgép abszolút sebessége, amely a keleti irányba mutat;
     - a repülőgép abszolút sebessége, amely az északi irányba mutat;
       - a repülőgép tartózkodási helyének szélessége.

ahol:
             - a keleti útsebesség;
  - a Föld (perifériás) kerületi sebessége.
Mivel , akkor a (22) egyenletből következik:

 (23 sz. egyenlet)

Behelyettesítve az  vektor értékét a (22) és az  vektor értékét a (23) egyenletekből a (21) egyenletbe és végrehajtva a vektoriális szorzásokat, kapjuk:

 
(24 sz. egyenlet)

Az axelerométerek ezen mutatásainak akkor lesz értelmük, ha az alap  tengelyei mentén lesznek elhelyezve, pontosan orientálva a vízszintes földrajzi koordináta rendszer  tengelyei mentén valamilyen eszközökkel. A  értékek (24), mint látható megkaphatjuk más módon is. Legyen az axelerométerek hármasa az objektum bármilyen alapján elhelyezve és tetszőlegesen forogjon az inerciális térhez képest. Ha a vektor mutatását  levetítjük a vízszintes földrajzi koordináta rendszer tengelyeire, akkor a vetületek értékei egyenlőek a (24) egyenletben leírtakkal.

4. A vízszintesen azimutálisan szabad alapra rögzített axelerométerek egyenletei
Az adott esetben a 4. ábrából kapjuk:

 (25 sz. egyenlet)
(26 sz. egyenlet)

Ha feltételezzük , akkor  és az (25), (26) egyenleteket behelyettesítve az (21) egyenletbe (esetén a (20) egyenletbe), kapjuk:

 (27 sz. egyenlet)

Nem nehéz megérteni, hogy ebben az esetben is () értékeket megkaphatjuk a mozgó objektum fedélzetén az axelerométer hármas mutatásának  levetítésével a vízszintesen azimutálisan szabad  koordináta rendszer tengelyeire.
Abban az esetben, ha az axelerométerek az  vízszintesen azimutálisan szabad koordináta rendszer tengelyei stabilizáltak és az ő tengelyeinek érzékenysége egybeesik az  tengelyekkel, akkor az axelerométerek mutatása a (27) egyenlettel lesz egyenlő.
Megjegyezzük, hogy a gyakorlatban a fedélzeten az axelerométerek  vetületeinek mutatásának mérése bármilyen  koordináta rendszerben, általában ezeket az axelerométereket az alapon helyezik el, amelyet a kiválasztott koordináta rendszer tengelyi mentén irányítanak. Az axelerométer hármas mutatásának levetítési módszere, akárhogyan is van elhelyezve az objektumon, az adott koordináta rendszer tengelyei mentén ritkán alkalmazzák.

Felhasznált irodalom

[1] Tóth János: Automatizált nagytávolságú léginavigáció. LRI Repülésoktatási Központ, 1994.
[2] В. А. Вериго, Ф. С. Гергель: Пилотажно-навигационные приборы и измерительные системы. Ленинградская Краснознаменная военно-воздушная инженерная академия имени А. Ф. Можайского, Ленинград, 1959.
[3] О. А. Бабич, В. А. Боднер, М. С. Козлов, М. Д. Потапов, В. П. Селезнев: Авиационные приборы и навигационные системы. ВВИА им. проф. Н.Е.Жуковского, Москва, 1969.

1. A repüléstudományi Közlemények 2008/2 számában megjelent Inerciális navigációs rendszerek I. cikk 4. ábrája alapján.
2. A repüléstudományi Közlemények 2008/2 számában megjelent Inerciális navigációs rendszerek I. cikk (1) egyenletéből következik.
3. A repüléstudományi Közlemények 2008/2 számában megjelent Inerciális navigációs rendszerek I. cikk.

Vissza a tartalomhoz >>>