Dr. Békési Bertold
ZMNE BJKMK Repülő és Légvédelmi Intézet Fedélzeti Rendszerek Tanszék
bekesi.bertold@uni-nke.hu

Inerciális navigációs rendszerek I.

Az inerciális navigációs rendszerek működésének elve a mechanikai jelenségek alkalmazásán alapszik, amely a test gravitációs mezejének mozgásakor lép fel.
A test mozgását ekkor valamely koordináta rendszer körül vizsgáljuk, amely maga mozog a világmindenséghez képest állandó sebességgel és forgás nélkül. Az ilyen koordinátarendszert nevezzük inerciálisnak.
A gyakorlati kérdések megvizsgálásakor, a földközeli vagy a napközeli tér kapcsolatban van a navigációval, az inerciális koordináta rendszer a „nem mozgó” csillagokkal van kapcsolatban. A szögmozgások a megfigyelő számára, amely a naprendszerben van nagyon kicsik.
Az inerciális navigációs rendszerek működésének alapjául mérések szolgálnak, amelyeket speciális berendezésekkel valósítunk meg, ezek kapták az axelerométer (gyorsulásmérő) nevet.

Az inerciális navigációs rendszerek működésének elve és koordináta rendszerei

Az ideális axelerométerek működési egyenlete, amely fontos szerepet játszik az inerciális rendszer elméletében a következő egyenlettel határozható meg:

                                       (1)

Ez az egyenlet összekapcsolja a  axelerométer mutatási vektorát, a repülőgép abszolút gyorsulásával , amelyben axelerométerek vannak elhelyezve és a repülőgép ugyanezen pontjában a gravitációs mező intenzivitását .
A navigációban a geometriai méreteket elszokás hanyagolni és anyagi pontnak vesszük, ezért feltételezhetjük, hogy az  vektort a repülőgép abszolút gyorsulásának foghatjuk fel, és a  vektort pedig a gravitációs mező intenzivitásának a repülőgép tartózkodási pontjában (1. ábra).
Tételezzük fel, hogy , amely minden gravitációs mezőre meghatározott. Továbbá figyelembe vesszük, hogy az abszolút gyorsulás az  rádiusz vektor első és második deriváltjának függvénye.


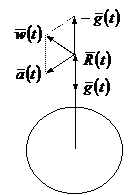
1. ábra.

Akkor az axelerométer mutatása az (1) egyenlet figyelembe vételével szintén a repülőgép koordinátáinak és ezek első és másodderiváltjainak lesznek a függvényei.

                                       (2)

A (2) egyenlet egy differenciális egyenlet, amelynek  szerinti megoldása az  kezdeti feltételekből határozza meg  és a mozgó repülőgép sebességi vektorát .
Ilyen módon tehát az axelerométer mutatásából (2) meghatározható:

Tehát a következőképpen csoportosíthatjuk az axelerométereket:

Koordináta rendszerek
Az -t nyugalmi helyzetben lévő koordináta rendszerben értjük, ezért a mérést az axelerométerek inerciális koordináta rendszerben hajtják végre ®  (2.ábra).
Ezt a koordináta rendszert általában úgy választják meg, hogy a középpontja egybeessen a Föld középpontjával. A  tengely a Föld saját forgásának irányába (körülbelül az égitestre), az  a tavaszpontra mutat, és az  pedig mindkettőre merőleges úgy, hogy jobbsodrású rendszert alkosson.
A repülőgép tartózkodási helyének pillanatnyi koordinátái a földrajzi vagy ortodróm koordináta rendszerben adható meg a legcélszerűbben.



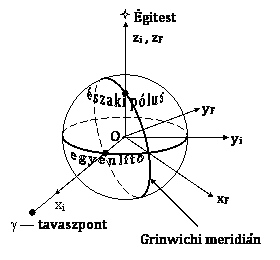
2. ábra.

A gyakorlati navigációban széles körű alkalmazásra tett szert a földrajzi koordinátarendszer (). A  tengely a Föld saját forgásának irányával egyezik meg. Az  tengely a grinwichi meridián és az egyenlítő metszéspontján halad át. Az  merőleges az tengelyekre. A földrajzi koordináták a szférikus értékekkel határozhatók meg, ezek a:

— szélesség
— hosszúság
R— a földtől való távolság

A földrajzi koordináta rendszer az inerciálishoz képest a Föld napi forgásával  sebességgel forog.


3. ábra

Ugyanakkor alkalmaznak ortodróm koordináta rendszert  (3. ábra). A földrajzitól annyiban különbözik csak, hogy az ortodróm egyenlítő síkja a földrajzi egyenlítő síkjához van hajlítva. Mint tudjuk az ortodróm egyenlítő az útvonal kezdeti és végpontján keresztül megy át. Az ortodróm koordináta rendszer úgy mint a földrajzi koordináta rendszer az inerciális koordináta rendszerhez képest  szögsebességgel forog. Ezen kívül széles alkalmazási lehetőséget kaptak az úgynevezett vízszintes koordinátarendszerek. Az alkalmazásuknak majd a gyakorlati szempontból lesz jelentős előnye, amelyeket majd később vizsgálunk.

A vízszintes koordináta rendszer középpontja nem a Föld középpontjával esik egybe, hanem az objektummal (például repülőgéppel) 4. ábra. A  tengely a helyi függőleges irányába mutat felfelé, az  és tengelyek a vízszintes síkban helyezkednek el. Ha az  tengely a földrajzi Északi pólus irányába mutat (vagyis az Északi pólus az  síkban fekszik), akkor a rendszert földrajzi vízszintes koordináta rendszernek hívjuk.


4. ábra.

Ha az  az ortodrómikus pólus irányába mutat, akkor a rendszert ortodrómikus vízszintes koordináta rendszernek hívjuk. Ha az  tengelyek tetszőlegesen vannak elhelyezve a vízszintes síkban és a rendszer abszolút szögsebessége  a függőlegesre vetülete van, amely nullával egyenlő, vagyis , akkor az ilyen koordináta rendszert azimutálisan vízszintesen szabad koordináta rendszernek hívjuk.
Végezetül megvizsgálunk még egy típusú koordinátarendszert. A középpontját egy pontba helyezik, amely az objektummal esik egybe, az  tengelyek az abszolút térhez képest nem forognak, vagyis =0. Speciális elnevezése nincsen ennek a koordináta rendszernek, de néha szokták nem forgónak nevezni.
Tehát különböző féle koordináta rendszerek kerültek bevezetésre. Milyen céllal? Az inerciális koordináta rendszerek az elméleti alapozásra szolgálnak. A földrajzi és ortodrómikus koordináta rendszerekben az objektum pillanatnyi koordinátáinak kiszámítása történik. A vízszintes és a nem forgó koordináta rendszerekben alapok dolgoznak, amelyeken az axelerométerek (gyorsulásmérők) vannak elhelyezve.

Felhasznált irodalom

[1] Tóth János: Automatizált nagytávolságú léginavigáció. LRI Repülésoktatási Központ, 1994.
[2] В. А. Вериго, Ф. С. Гергель: Пилотажно-навигационные приборы и измерительные системы. Ленинградская Краснознаменная военно-воздушная инженерная академия имени А. Ф. Можайского, Ленинград, 1959.
[3] О. А. Бабич, В. А. Боднер, М. С. Козлов, М. Д. Потапов, В. П. Селезнев: Авиационные приборы и навигационные системы. ВВИА им. проф. Н.Е.Жуковского, Москва, 1969.

Vissza a tartalomhoz >>>