Dr. Békési Bertold
egyetemi docens
ZMNE BJKMK RLI Fedélzeti Rendszerek Tanszék
bekesi.bertold@uni-nke.hu
ZÁRT GIROINERCIÁLIS NAVIGÁCIÓS RENDSZEREK DINAMIKÁJA, SZERKEZETI HIBÁI
Zárt giroinerciális navigációs rendszerek dinamikája
A kérdés megvizsgálásához a giroinerciális alapú differenciális mozgásegyenletet állítunk össze. Itt is csak a vízszintesen azimutálisan szabad alapú esetet vizsgáljuk. Ezen eset megvizsgálása után más vízszintes alapú rendszerekre is kiterjeszthetjük. Tételezzük fel, hogy a giroinerciális rendszer vízszintes tengelyei az x és y vízszintesen azimutálisan szabad koordinátarendszer kis 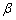 és
és 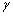 szögekkel eltérnek (1. ábra).
szögekkel eltérnek (1. ábra).

1. ábra
Az 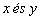 vízszintesen azimutálisan szabad koordináta-rendszer kis
vízszintesen azimutálisan szabad koordináta-rendszer kis  és
és 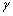 szögekre eltérítve [5]
szögekre eltérítve [5]
[Szerk.: Dr. Békési Bertold – MS Word]
Az axelerométerek érzékelő tengelyei egybeesnek az alap tengelyeivel 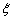 és
és 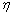 (1. ábra és 4. ábra ). Hasonlóan már a nyitott inerciális navigációs rendszerek egyenletéhez megkapjuk, hogy az axelerométerek jelzései a következő értékekkel rendelkeznek.
(1. ábra és 4. ábra ). Hasonlóan már a nyitott inerciális navigációs rendszerek egyenletéhez megkapjuk, hogy az axelerométerek jelzései a következő értékekkel rendelkeznek.
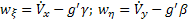 (1)
(1)
Csak a 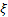 tengelyre vizsgáljuk meg és ennek a hatásvázlata a 2. ábrán látható.
tengelyre vizsgáljuk meg és ennek a hatásvázlata a 2. ábrán látható.
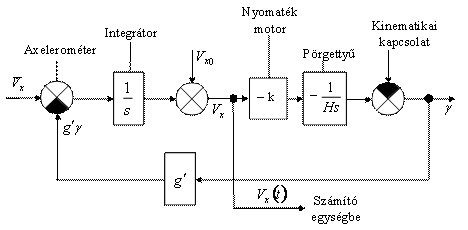
2. ábra
Zárt giroinerciális navigációs rendszer hatásvázlata [5]
[Szerk.: Dr. Békési Bertold – MS Word]
A kinematikai kapcsolat (2. ábra) figyelembe veszi a helyi függőleges elfordulását a repülőgép mozgásakor. A kinematikai jelkapcsolat értéke a következő:
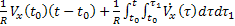 (2)
(2)
Az (1) pörgettyűre (2, 4. ábrák) a
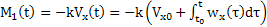 (3)
(3)
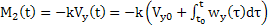 (4)
(4)
egyenletekkel egyetértve, nyomaték hat.
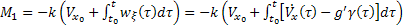 (5)
(5)
A nyomaték hatására az alap precesszálni kezd a 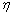 tengely körül
tengely körül 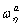 szögsebességgel:
szögsebességgel:
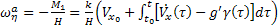 (6)
(6)
Figyelembe véve, hogy az alap x tengely körüli szögsebessége
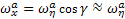 (7)
(7)
és a Schuler feltétel 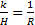 , kapjuk
, kapjuk
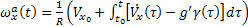 (8)
(8)
A különbség az 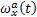 és az
és az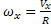 között a
között a 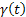 hiba sebesség növekedése következtében
hiba sebesség növekedése következtében
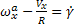 (9)
(9)
A (8) és (9) egyenletekből következik, hogy
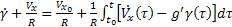 (10)
(10)
Differenciálva a (10) egyenletet „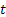 ” szerint, megkapjuk az alap differenciális mozgásegyenletét a vizsgált giroinerciális rendszerre.
” szerint, megkapjuk az alap differenciális mozgásegyenletét a vizsgált giroinerciális rendszerre.
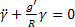 (11)
(11)
kezdeti feltételek mellett
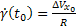 ;
; 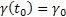 (12)
(12)
ahol:
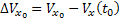 — a sebesség kezdeti értékének bevezetési hibája;
— a sebesség kezdeti értékének bevezetési hibája;
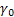 — az alap vízszintesbe történő beállításának hibája.
— az alap vízszintesbe történő beállításának hibája.
Tehát a giroinerciális rendszer alapjának mozgása csillapítatlan lengést képvisel 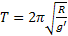 Schuler periódussal és
Schuler periódussal és 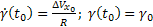 kezdeti feltételek esetén.
kezdeti feltételek esetén.
Megoldva a (10) egyenletet, kapjuk:
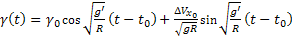 (13)
(13)
A 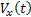 sebesség kiszámításának hibája
sebesség kiszámításának hibája
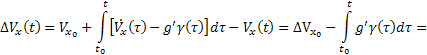
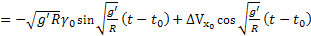 (14)
(14)
Tehát:
A giroinerciális alap mindkét vízszintes csatornában dinamikai tekintetben Schuler-periódusú lengő tag. Az inerciális navigációs rendszer alapja a stabilitás határán lévő rendszer.
Olyan rendszer létrehozása, amelynek saját mozgása asszimptótikusan stabilis, vagyis időben csillapodó, nem lehetséges.
Bármilyen csillapító tag bevezetése a rendszerbe azonnal hibához vezet a koordináták meghatározásában, mivel olyankor a rendszer ballisztikusan zavarhatóvá válik, vagyis dinamikus hibák jelennek meg a repülőgép manőverei közben.
Ahhoz, hogy az inerciális navigációs rendszer saját mozgása asszimptótikusan stabilis legyen és ne rendelkezzen dinamikus hibával a koordináták kiszámításakor, csak akkor lehetséges ha más fedélzeti rendszerek információt juttatnak a rendszerbe a repülőgép mozgásáról.
Zárt vízszintes alapú inerciális navigációs rendszerek szerkezeti hibái
Először megvizsgáljuk, hogy az elemek szerkezeti hibái hogyan hatnak a giroinerciális rendszer hatásvázlatára és a hibáira, amelyek a következők:
- a vízszinteshez képest az alap szögelfordulása;
- a sebesség kiszámításának hibái;
- a mozgó objektum kiszámításának hibái.
Itt csak a pörgettyű elvándorlásából és az integrátorok driftjéből eredő hibák vizsgálatára korlátozódunk. Az előzőekhez képest itt is csak a vízszintes csatornát vizsgáljuk meg. A hibaképződés folyamata a csatornában a következő hatásvázlaton látható (3. ábra).
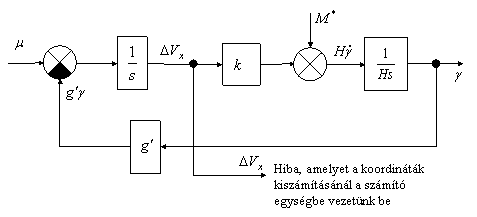
3. ábra
A hibaképződés folyamatának hatásvázlata [5]
[Szerk.: Dr. Békési Bertold – MS Word]
ahol:
- nyomaték, amely a pörgettyű elvándorlását eredményezi;
- az integrátor driftje.
A 3. ábra a 2. ábrából következik, a bemeneti jel és a kezdeti feltétel jelét kompenzáltnak tekintjük a kinematikai kapcsolattal. A hatásvázlatból a következő egyenlet következik:
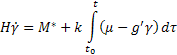 (15)
(15)
Ez az egyenlet írja le a hibaképződés folyamatának dinamikáját. Ha feltételezzük, hogy és állandóak az időben.
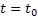 feltétel mellett a (15) egyenletből kapjuk
feltétel mellett a (15) egyenletből kapjuk
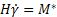 (16)
(16)
Ha differenciáljuk a (15) egyenletet az időben a Schuler-feltétel segítségével , akkor a következő differenciál egyenletet kapjuk:
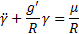
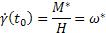
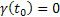 (17)
(17)
ahol: - a pörgettyű elvándorlásának szögsebessége
A (17) differenciál egyenlet megoldása a kezdeti feltételek mellett:
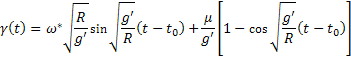 (18)
(18)
Ebben az esetben a 3. ábrából kapjuk, hogy a hiba
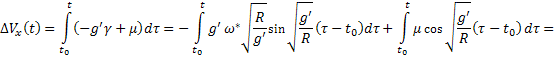
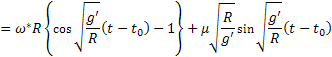 (19)
(19)
A (19) kifejezésből kapjuk a repülőgép meghatározási koordinátájának hibáját az x tengely mentén:
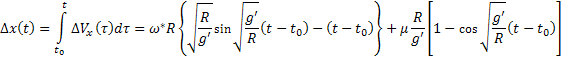 (20)
(20)
Tehát a m integrátor állandó driftje állandó és lengő hibákat eredményez az alap helyzetében a vízszinteshez képest (17), az objektum koordinátáinak kiszámításában (19), a mozgó objektum sebességének meghatározásában (18). A pörgettyű állandó elvándorlása lengő hibát eredményez az alap helyzetében (20) és a hiba állandó összetevőjének megjelenéséhez vezet a sebesség meghatározásában (18) és a hiba lineárisan növekvő összetevőjében és a mozgó objektum koordinátáinak meghatározásában (19).
Ha az időben a hiba növekedését összehasonlítjuk a zárt és nyitott inerciális navigációs rendszereknél, akkor rögtön érthető lesz a zárt inerciális navigációs rendszerek előnye. Valóban a zárt inerciális navigációs rendszerek hibája a koordináta megállapításánál, amely a pörgettyű elvándorlását eredményezi, lineárisan változik az időben, a nyitott inerciális navigációs rendszereknél ugyanazon feltételek mellett (a pörgettyű állandó elvándorlása - az alapok stabilizátorjai) az idő köbével arányos.
Meghatározzuk a korrelációs mátrixot
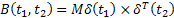 (21)
(21)
ahol: - a matematikai teljes valószínűség jele
- a mátrix transzponáltjának a jele
A hiba vektorát
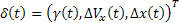 (22)
(22)
Feltételezzük, hogy a és zavaró hatások az időben állandó véletlen vektort eredményeznek nulla matematikai teljes valószínűséggel és korrelációs mátrixxal
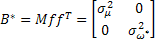 (23)
(23)
ahol: és - az integrátor és a pörgettyű elvándorlás szórásnégyzetének driftje (elsodródása)
A hiba vektor összhangban a (17), (18) és (19) a zavaró vektoron keresztül lineárisan kifejezhető:
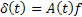 (24)
(24)
ahol a mátrix
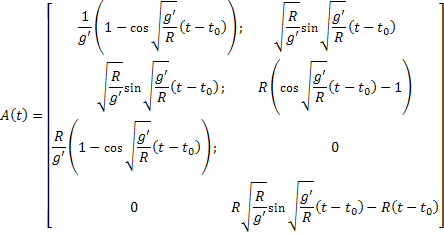 (25)
(25)
Ebben az esetben kapjuk
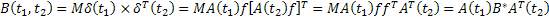 (26)
(26)
Ha a korrelációs mátrixban a , akkor a hiba kovariáns mátrixát kapjuk , amelyek diagonális elemei (tagjai) a hiba szórásnégyzete lesz . Érthető, hogy ezek a szórásnégyzetek a t idő funkciói lesznek, tehát az inerciális rendszer hibái véletlen nemstacionárius (helyhez kötött) folyamat.
Zárt giroinerciális navigációs rendszerek vízszintes földrajzi alappal
Az inerciális rendszernek ez a típusa elméletileg nem különbözik a fentebb vizsgált vízszintesen azimutálisan szabad alapú giroinerciális navigációs rendszertől.
Az alap vízszintességének feltételei, hasonlóak a Repüléstudományi Közlemények 2009/1 számában megjelent „Zárt vízszintes alapú inerciális navigációs rendszerek” cikk (1) és (2) feltételeknek, ebben az esetben [lásd a Repüléstudományi Közlemények 2008/3 számában megjelent Inerciális navigációs rendszerek II. cikk 22 egyenletét)] a következő alakot veszik fel
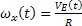 (27)
(27)
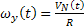 (28)
(28)
ahol: 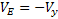 és
és 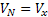 - az objektum abszolút sebességének keleti és északi összetevői.
- az objektum abszolút sebességének keleti és északi összetevői.
A (27) és (28) feltételek megvalósítása, az 1 és 5 (2.ábra) vízszintes pörgettyű házának függőleges tengelyeire 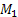 és
és 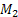 nyomatékokat helyezünk, amelyek a
nyomatékokat helyezünk, amelyek a 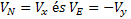 sebességekkel arányosak. Akkor figyelembe véve egyenleteket és a hatásvázlatot , kapjuk
sebességekkel arányosak. Akkor figyelembe véve egyenleteket és a hatásvázlatot , kapjuk
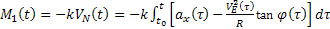 (29)
(29)
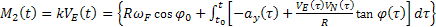 (30)
(30)
Egyértelmű, hogy ebben az esetben a jeleket integrálni, amelyeket az axelerométerektől kapunk, tilos. Először az axelerométerek mutatásaiból ki kell vonni a 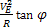 és
és 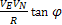 módszeres hibákat, amelyek az objektum koordinátáinak és sebességeinek elég bonyolult összefüggései.
módszeres hibákat, amelyek az objektum koordinátáinak és sebességeinek elég bonyolult összefüggései.
A „módszeres hibák” kompenzálásának mechanizmusa nagy hátránya a földrajzi alapú inerciális rendszereknek az azimutálisan szabad alapú inerciális rendszerekkel szemben.
A feladat, hogy az inerciális navigációs rendszerek működési stabilitásának elemzésekor a kompenzáló mechanizmust figyelembe vegyük igen nehéznek tűnik és ezt itt nem fogjuk megvizsgálni. Továbbá a stabilitás elemzése a kompenzáló mechanizmus figyelembe vétele nélkül mint látható a fentebb vizsgált dinamikai inerciális kontúrral vezethető le, amely a 2. ábrán látható.
Végezetül ebben az esetben az iránypörgettyű nem azimutálisan szabad, hanem az irányszögrendszertől olyan módon helyesbítődik, hogy az ő tengelyének alakja mindig a meridián síkjában van elhelyezve.
Asztroinerciális navigációs rendszerek
Két típust vizsgálunk meg:
- az inerciális térben változatlan helyzetű nem forgó alappal;
- vízszintes alappal.
Két teleszkóp segítségével, amelyek a csillagok felé vannak irányítva (4. ábra) az alappal, amelyen 3 darab axelerométer található, amely úgy van stabilizálva, hogy az egyik tengely érzékenysége a világtengely (z tengely) felé van irányítva, a másik - a 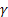 tavaszpontba (x tengely) és a harmadik - az első kettőre merőlegesen (y tengely). Ilyen típusú alapot már vizsgáltunk a Repüléstudományi Közlemények 2008/3 számában megjelent Inerciális navigációs rendszerek II. cikkben. Ha most ezeknek az axelerométereknek a mutatását bevezetjük a 4. ábra [5] bemenetére, amelyek saját frekvenciája egyenlő a Schuler frekvenciával
tavaszpontba (x tengely) és a harmadik - az első kettőre merőlegesen (y tengely). Ilyen típusú alapot már vizsgáltunk a Repüléstudományi Közlemények 2008/3 számában megjelent Inerciális navigációs rendszerek II. cikkben. Ha most ezeknek az axelerométereknek a mutatását bevezetjük a 4. ábra [5] bemenetére, amelyek saját frekvenciája egyenlő a Schuler frekvenciával 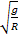 , akkor ezeknek a tagoknak a kimenetén
, akkor ezeknek a tagoknak a kimenetén 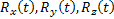 rádiusz vektor pillanatnyi koordinátáit kapjuk meg.
rádiusz vektor pillanatnyi koordinátáit kapjuk meg.
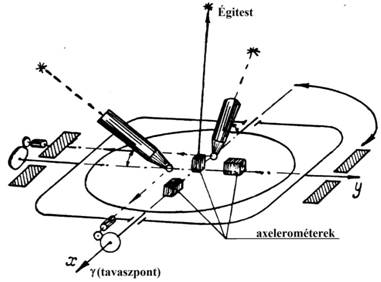
4. ábra
A feladat most abból áll, hogy a rádiusz-vektor mentén
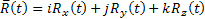 (31)
(31)
adott nem forgó koordináta rendszerben, kiszámítani a földrajzi illetve minden másfajta koordinátát, amelyet a repülőgép gyakorlati navigációjában alkalmaznak.
Az 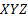 koordináta rendszer tengelyei párhuzamosak az
koordináta rendszer tengelyei párhuzamosak az 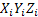 inerciális rendszer tengelyeivel, amelyek középpontja a Föld középpontjában helyezkedik el . Ilyen esetben a szögek, amelyet az
inerciális rendszer tengelyeivel, amelyek középpontja a Föld középpontjában helyezkedik el . Ilyen esetben a szögek, amelyet az 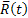 vektor hoz létre
vektor hoz létre 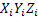 koordináta rendszer tengelyeivel, egyenlő az
koordináta rendszer tengelyeivel, egyenlő az 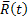 vektor és az
vektor és az 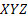 koordináta rendszer tengelyeinek megfelelő szögei között.
koordináta rendszer tengelyeinek megfelelő szögei között.
Vizsgáljuk meg az 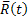 szöghelyzetét az inerciális koordináta rendszerhez
szöghelyzetét az inerciális koordináta rendszerhez 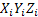 képest. (5. ábra)
képest. (5. ábra)

5. ábra
Az 5. ábrából következik, hogy a repülőgép helyi csillagideje egyenlő:
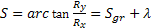 (32)
(32)
és a hely szélessége
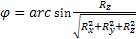 (33)
(33)
Tehát a repülőgép fedélzetén lévő kronométer (időmérő, pontos óra), amelynek segítségével meghatározható a grinwichi csillagidő 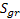 , az
, az 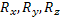 rádiusz vektor koordináták alapján lehet meghatározni a
rádiusz vektor koordináták alapján lehet meghatározni a 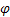 és
és 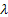 földrajzi koordinátákat. Tehát most megvizsgáltuk a zárt asztroinerciális navigációs rendszer működési elvét az inerciális térhez képest nem forgó alappal.
földrajzi koordinátákat. Tehát most megvizsgáltuk a zárt asztroinerciális navigációs rendszer működési elvét az inerciális térhez képest nem forgó alappal.
Most röviden vizsgáljuk meg a zárt asztroinerciális navigációs rendszer működési elvét vízszintes alappal.
A két teleszkóp segítségével (6. ábra) a csillagászati blokk stabilizálva van az inerciális térhez képest. Az alap, amelyen az axelerométerek vannak elhelyezve a csillagászati blokkhoz képest elfordulhat. Csak az egyik csatornát vizsgáljuk meg itt is (6. ábra) [5].
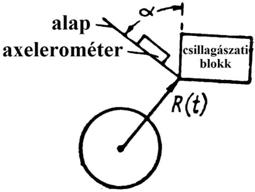
6. ábra
Az axelerométer a vízszintes síkban helyezkedik el. Ha a kezdeti időpillanatban az alap vízszintes helyzetű, akkor az alap elfordulási szögét 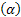 az axelerométer jelének kétszeres integrálása után kapott jellel arányosan helyesbítve és figyelembe véve az alap
az axelerométer jelének kétszeres integrálása után kapott jellel arányosan helyesbítve és figyelembe véve az alap 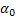 kezdeti szögét és a
kezdeti szögét és a 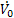 kezdeti sebességet, az arányossági tényezőt pedig
kezdeti sebességet, az arányossági tényezőt pedig 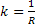 értékére választva az alap az axelerométerrel minden időben vízszintes marad, az objektum bármilyen törvényszerű mozgása esetén. Tehát az alap ballisztikusan nem lesz zavarható. Valójában, ebben az esetben kapjuk:
értékére választva az alap az axelerométerrel minden időben vízszintes marad, az objektum bármilyen törvényszerű mozgása esetén. Tehát az alap ballisztikusan nem lesz zavarható. Valójában, ebben az esetben kapjuk:
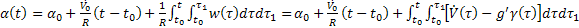 (34)
(34)
ahol:
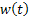 - az axelerométer mutatása
- az axelerométer mutatása
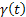 - az alap eltérési szöge a vízszintes síkhoz képest (az alap szöghelyzetében hiba)
- az alap eltérési szöge a vízszintes síkhoz képest (az alap szöghelyzetében hiba)
Figyelembe véve a 6. ábrából 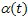 szög egyenlő:
szög egyenlő:
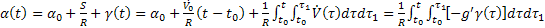 (35)
(35)
és hogy
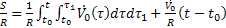 (36)
(36)
a repülőgép elmozdulásának szöge a mozgás vizsgált síkjában, akkor az (35) kapjuk 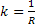 esetén
esetén
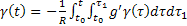 (37)
(37)
Kétszeres differenciálás után az idő szerint az (37) egyenletből kapjuk:
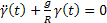 (38)
(38)
A (38) egyenletből következik, hogy dinamikailag a zárt asztroinerciális navigációs rendszer vízszintes alappal egy lengő tagot eredményez, amelynek a saját frekvenciája egyenlő a Schuler periódusával.
A 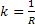 lesz a Schuler-feltétel az adott asztroinerciális rendszerre.
lesz a Schuler-feltétel az adott asztroinerciális rendszerre.
Ha az alap kezdeti eltérése elég kicsi lenne, akkor a továbbiakban az eltérés ezen értéke a szerkezeti hibák figyelembe vétele nélkül ne fogja meghaladni a kezdetit. Az axelerométer mutatását integrálva a kezdeti feltételek figyelembe vételével, megkapjuk a repülőgép sebességét a vizsgált mozgási síkban. A repülőgép sebességét integrálva, a kezdeti feltételek figyelembe vételével megkapjuk a koordinátáit.
Az asztroinerciális rendszerek hibái a giroinerciális rendszer hibáihoz képest az idővel nem nőnek. Ez abból következik, hogy a teleszkópos rendszer, amely megvalósítja az inerciális koordináta rendszert, hibával rendelkezik, amely az idővel nem nő, nem úgy mint a pörgettyűs rendszer, amely egy meghatározott koordináta rendszert határoz meg, amely a pörgettyű driftje miatt nem folyamatosan fordul el, vagyis hibával rendelkezik - az idővel arányosan nő. A fentebb említett elv nagy előnye az asztroinerciális rendszereknek.
Repüléstudományi Közlemények 2009/1 számában megjelent „Zárt vízszintes alapú inerciális navigációs rendszerek” cikk 4. ábrája.
Repüléstudományi Konferencia 2009 Szolnok 50 év hangsebesség felett a Magyar légtérben megjelent „Nyitott vízszintes alapú inerciális navigációs rendszerek” cikk 12 és 13 egyenletei.
A repüléstudományi Közlemények 2009/1 számában megjelent „Zárt vízszintes alapú inerciális navigációs rendszerek” cikk 2 és 4. ábrája alapján
lásd a Repüléstudományi Közlemények 2008/3 számában megjelent Inerciális navigációs rendszerek II. cikk 20 egyenletét.
a Repüléstudományi Közlemények 2009/1 számában megjelent „Zárt vízszintes alapú inerciális navigációs rendszerek” cikk 2. és 4. ábrái alapján.
a Repüléstudományi Közlemények 2009/1 számában megjelent „Zárt vízszintes alapú inerciális navigációs rendszerek” cikk 4 és 5 egyenleteket.
a Repüléstudományi Konferencia 2009 Szolnok 50 év hangsebesség felett a Magyar légtérben megjelent „Nyitott vízszintes alapú inerciális navigációs rendszerek” cikk 3. ábráját.
a Repüléstudományi Közlemények 2009/1 számában megjelent „Zárt vízszintes alapú inerciális navigációs rendszerek” cikk 4. ábrája.
lásd a Repüléstudományi Közlemények 2008/2 számában megjelent Inerciális navigációs rendszerek I. cikket
Felhasznált irodalom
[1] Dr. Békési Bertold: Inerciális navigációs rendszerek I. Repüléstudományi Közlemények online folyóirat, Szolnok, 2008/2 szám. HU ISSN 1789-770X
[2] Dr. Békési Bertold: Inerciális navigációs rendszerek II. Repüléstudományi Közlemények online folyóirat, Szolnok, 2008/3 szám. HU ISSN 1789-770X
[3] Dr. Békési Bertold: Zárt vízszintes alapú inerciális navigációs rendszerek. Repüléstudományi Közlemények online folyóirat, Szolnok, 2009/1 szám. HU ISSN 1789-770X
[4] Dr. Békési B. — Dr. Szegedi P. Nyitott vízszintes alapú inerciális navigációs rendszerek. Repüléstudományi Közlemények különszám, Szolnok, 2009. április 24. (CD-ROM).
[5] В. А. Вериго, Ф. С. Гергель: Пилотажно-навигационные приборы и измерительные системы. Ленинградская Краснознаменная военно-воздушная инженерная академия имени А. Ф. Можайского, Ленинград, 1959.


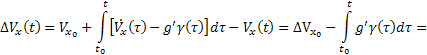

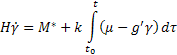 (15)
(15)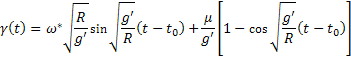 (18)
(18)
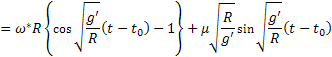 (19)
(19)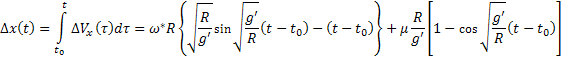 (20)
(20)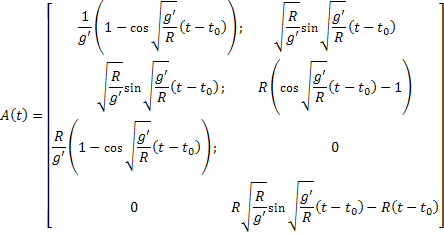 (25)
(25)

